ML - Theory #12 : 서포트 벡터 머신 (Support Vector Machine, SVM)

아래 그림과 같이 데이터를 분리할 decision boundary인 hyperplane을 찾아야한다. 여기서 초평명(hyperpalne)은 최대 마진 분류기가 선형 경계로 사용하는 선으로 임의의 공간을 반으로 양분하는 선이다. 2차원 공간에서의 초평면은 1차원 직선이고, 3차원 공간에서의 초평면은 2차원 평면이다.

 

예를 들면 아래와 같은 빨간색 실선인 hyperplane으로 데이터를 분리할 수 있다.

아니면 아래와 같은 빨간색 점선인 hyperplane으로 데이터를 분리할 수도 있다.

이렇게 구분이 가능한 즉 분리가 가능한 초평면이 두 개 이상인 hyperplane이 존재한다면, 이것을 separating hyperplane이라 부른다. 즉, 아래 그림처럼 분리가 가능한 초평면이 하나가 아닌 여러개인 경우, 관측치들을 클래스 라벨에 따라 완벽하게 분리하는 초평면들이다.

 

 

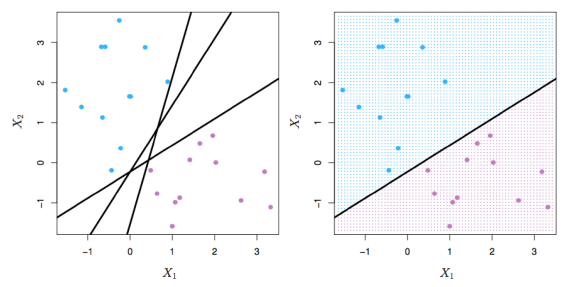
하지만, separating hyperplane 중에 어떤 hyperplane이 데이터를 잘 구분하는 것인지 어떻게 판단할 수 있을까? 그렇기 때문에 우리는 SVM을 이용하여 판단하게 된다. SVM은 선형 SVM과 비선형 SVM으로 나뉜다.

 

• 선형 SVM (Linear SVM)
  • 최대 마진 분류기(Max-margin classifier) using 하드 마진(hard margin)
  • 서포트 벡터 분류기(Support Vector Classifier, SVC) using 소프트 마진(soft margin)
• 비선형 SVM (Nonlinear SVM)
  • 커널 SVM

위에 리스트 되어있는 것들을 본 글에서 차근차근 알아보도록 한다.

 

최대 마진 분류기 (Max-margin classifier)

분리 초평면(Separating hyperplane) 중, 훈련 관측치로부터 가장 멀리 떨어진(=제일 큰 margin을 갖는) 초평면(Hyperplane)을 기준으로 분류하는것을 의미한다. margin은 두 종류의 margin으로 나뉜다: 하드 마진(hard margin), 소프트 마진(soft margin).

▶ 서보트 벡터 ◀

• hyperplane으로부터 margin 크기 만큼 떨어진 실선에 걸쳐있는 관측값

 ▶ 마진 (Margin) ◀

• decision boundary로부터 가장 가까운 데이터(=서포트벡터, support vector)까지의 거리를 의미한다. 즉, 각각의 데이터 벡터들과 hyperplane까지의 거리 중, 가장 짧은 거리를 마진(Margin)이라 한다. 마진이 작을 수록, 작은 변화에도 관측값들의 결과값이 달라짐으로써 overfitting이 될 가능성이 있다. 반면, 마진이 클 수록, generalization error가 낮아지는 경향을 보임으로써 관측값들을 완벽하게 분류할 수 있다. 그러므로 마진을 최대화하는 hyperplane을 선택하는 것이 더 좋은 분류를 하게 된다.

▶ 소프트 마진 (soft margin) ◀

• 하드 마진(hard margin)과는 달리 이상치(outliers)가 margin안에 어느 정도 포함되도록 하는 것을 의미한다. 그러므로 이상치(outliers)에 민감한 하드 마진(hard margin)과는 달리 소프트 마진(soft margin)은 이상치(outliers)에 민감하지 않다.

서포트 벡터 분류기 (Support Vector Classifier, SVC)

앞서 설명했던 최대 마진 분류기의 경우, 어떤 데이터에 대해서는 hyperplane이 존재하지 않을 수 있으며 그에 따라 최대 마진 분류기 또한 존재하지 않을 수 있다는 한계가 있다. 

이를 해결하기 위해 소프트 마진(soft margin)을 이용하여 약간의 오류를 허용함으로써, 관찰값들을 분류한다. 몇몇 관측치를 잘못 분류하더라도 나머지 관측치들을 더 잘 분류할 수 있는 방법이다. 즉, 아래의 그림에서 보이는 C(regularization parameter)를 이용하여 약간의 오류를 허용함으로써 과적합(Overfitting)을 방지한다. 그러므로 C가 커질수록 margin 폭이 좁아진다. 왜냐하면 margin을 줄이는 대신 margin 사이에 존재하는 데이터 그리고 틀린 데이터의 수를 줄이겠다는 의미이기 때문이다.  반대로 C가 작아질수록 margin 폭이 넓어진다. 그러므로 SVM모델이 과적합(Overfitting)되는 경우, C를 감소시켜 모델을 규제해야한다.

그러므로 soft margin을 최대화 하는 것과 outlier를 최소화 하는 것은 tradeoff관계이며, C를 통하여 margin과 error의 trade-off를 조절한다.

위의 설명을 이용하여 아래의 그림에서 C(regularization parameter)를 내림차순으로 나열하게되면 어떻게 나열될까? 답은 아래의 접은글에 작성되어있습니다 :)

>>> 답 : 4사분면 -> 3사분면 -> 1사분면 -> 2사분면

 

커널 서포트 벡터 머신 (Kernel Support Vector Machine, Kernel SVM)

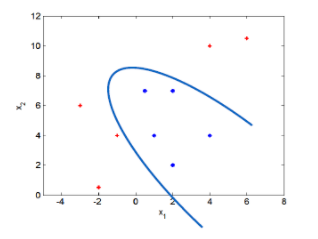
서포트 벡터 분류기에서 확장된, 비선형의 클래스 경계를 수용하는 분류 방법이다. 즉, 아래 그림과 같이 decision boundary가 비선형일 경우에 선형분류기를 비선형 구조로 변경해서 관측값들을 분류하기 위해 사용하는 방법이다.

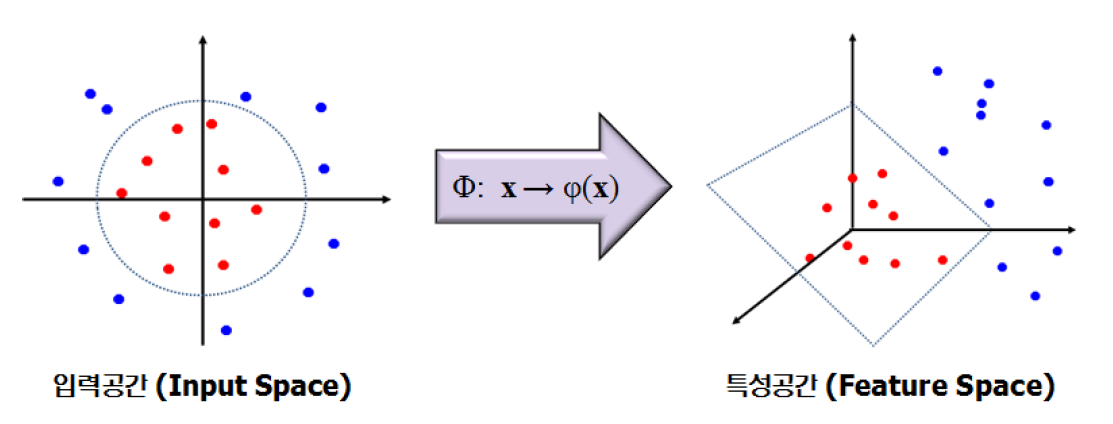
비선형 구조로 변경하기 위해 아래 그림처럼 입력 공간(Input space)을 학습 데이터의 선형 분리가 가능한 고차원 특성 곤간(Feature space)으로 mapping이 가능하도록 한다. 즉, 커널(kernel)을 사용하여 특정한 방식으로 변수공간을 확장한 방법이다. 그러므로 서포트 벡터 머신은 서포트 벡터 분류기와 커널을 사용한 방법이다.

고차원 공간에서의 선형 분리는, 입력 공간에서의 비선형 분리로 표현될 수 있다.

 

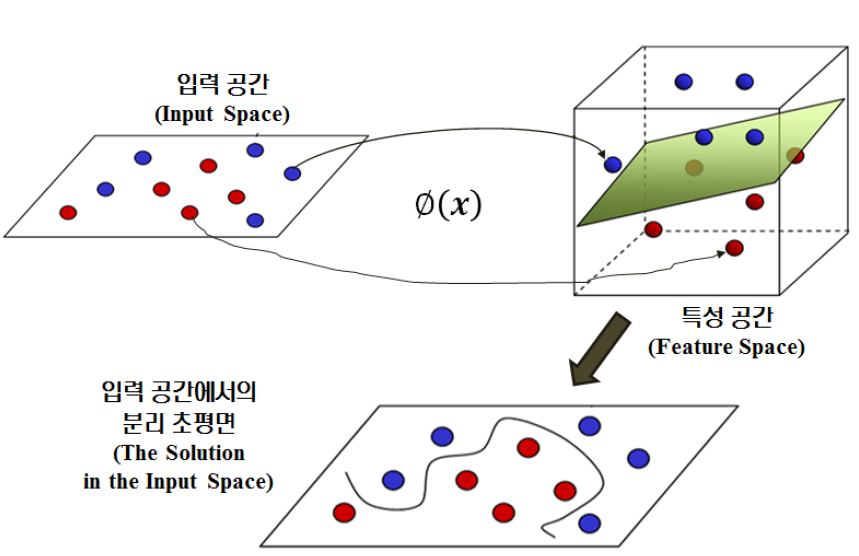
 ▶ 커널 (kernel) ◀

• 클래스들 사이의 비선형 경계를 수용하기 위해 변수 공간을 확장하고자 할 때 사용하는 계산기법으로 저차원 공간을 고차원 공간으로 매핑시켜주는 작업이다.

---

>> 위 내용은 필자가 공부하여 직접 정리한 내용이며, 위 그림 역시 직접 그린 그림이므로 워터마크 "s5unnyjjj"를 삽입하였음을 알려드립니다.

>> 부족한 점이 많을 수 있기에 잘못된 내용이나 궁금한 사항이 있으면 댓글 달아주시기 바랍니다.

>> 긴 글 읽어주셔서 감사합니다.