s5unnyjjj's LOG
ML - Practice #2 : Perceptron, Logistic Regression, KNN 본문
ML - Practice #2 : Perceptron, Logistic Regression, KNN
s5unnyjjj 2021. 8. 15. 22:15본 글에서는 아래에 나열된 이론을 바탕으로 코드를 작성해보도록 한다.
1. Perceptron (참고링크) https://s5unnyjjj.tistory.com/39?category=939071
2. Logistic Regression (참고링크) https://s5unnyjjj.tistory.com/39?category=939071
3. KNN (K-Nearest Neighbors) (참고링크) https://s5unnyjjj.tistory.com/63?category=939071
Used train data
사용할 데이터는 data_train.txt파일에 담겨 있다. 해당 파일을 열어보면 아래와 같이 저장되어있다.

아래의 코드를 이용하여 data_train.txt 파일에서 데이터를 불러온 후, 1행은 test1으로 2행은 test2로 이름을 부여하고 마지막 행인 3행은 Accepted 이름을 부여함으로써 Accepted 여부를 표시하도록 한다. data_train.txt파일을 보면 마지막 행에는 0과 1로 표시가 되어있는데, 1은 accepted을 의미하고 0은 Not accepted을 의미한다.
그렇게 되면 trainData의 5개의 값만 보게되면 아래와 같이 보여진다.

trainData의 값들은 아래와 같이 분포 되어 있다.

trainData의 test1과 test2값들을 하나의 배열로 묶은 후 trainX라 정의하고, Accepted값들은 trainY라 정의한다. trainX 값과 trainY 값은 80개이며, shape은 (80, 2)이다. trainX의 shape을 한 차원 증가시키고 첫 행은 1로 초기화 시키면 trainX의 shape은 (80, 3)이다. trainX의 5개의 값만 보게되면 아래와 같이 보여진다.

이로써 우리는 data_train.txt 파일 내에 있는 값들을 전처리 시킨 값을 trainX, trainY라 정의하였으며, trainX의 shape은 (80, 3)로 변경하였다. 이제부터는 trainX와 trainY를 이용하여 코드를 직접 구현해보도록 한다.
Perceptron
Perceptron를 구현하기위하여 가설함수와 비용함수에 대해서 먼저 알아본다. (개념은 아래 더보기에 있음)
가설함수(hypothesis) vs 비용함수(cost function)
가설함수(hypothesis)는 training dataset에 없는 새로운 데이터를 입력으로 넣었을 때 예측되는 출력을 도출하도록 하는 함수이다.
비용함수(cost function)는 predict value와 target value의 오차가 작은 가설함수를 도출하기 위해 사용되는 함수이다.
Perceptron의 가설함수 전체 식은 아래와 같다.

Perceptron의 비용함수 전체 식은 아래와 같다.

Peceptron의 theta를 update 식은 아래와 같으며, linear regression gradient descent와 유사한 것을 확인할 수 있다. (참고링크) https://s5unnyjjj.tistory.com/69?category=939071
하지만 식은 다르다는 것을 알아둬야한다. 왜냐하면 미분전 식에 포함된 가설함수의 정의가 다르기 때문이다.
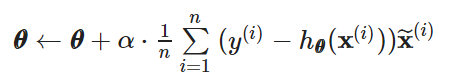
Perceptron_model.py 하위에 있는 perceptron 함수
perceptron 함수에는 Pecetpron의 가설함수(hypothesis)을 구현한다. 구현하면 아래와 같다.

Perceptron_model.py 하위에 있는 perceptron_cost 함수
perceptron_cost 함수에는 Pecetpron의 비용함수(cost function)을 구현한다. 구현하면 아래와 같다.

Perceptron_model.py 하위에 있는 update_perceptron 함수
update_perceptron 함수에는 theta를 업데이트 하는 코드를 구현한다. 구현하면 아래와 같다.

Result : Check results as iteration increases
처음에 theta를 [-400, 5, 1] 이라고 초기화시켜준다.

초기화 시킨 상황에서 비용함수의 값은 아래와 같이 출력되는 것을 확인할 수 있다.

이후 위에서 초기화 시킨 theta에서 비용함수의 값이 줄어들도록 theta를 update하게된다면 업데이트된 theta값은 아래와 같이 출력되는 것을 확인 할 수 있다.

위에서는 theta를 한번만 update 시킨 값이 출력된 것이다. 이제부터는 cost가 줄어들도록 최적화시킴으로써 최적화된 theta값을 확인해볼 것이다. 100번의 iteration동안 업데이트되도록하였으며, 100번의 iteration동안 만약 cost값이 0.1보다 작거나 updated된 theta를 이용하여 구한 cost값을 이전 cost값으로 나눴을 때 1보다 클경우에는 수렴되었다고 판단하여 업데이트를 중지시키도록 코드를 구현한 결과는 아래와 같다.

총 39번의 iteration동안 업데이트된 최적의 theta값은 아래와 같이 출력되는 것을 확인할 수 있다.

그래프로 시각화하해보면 아래와 같은 그래프를 확인할 수 있다. 해당 그래프를 보면 얇은 점선으로 되어있는 것은 무작위로 설정함으로써 초기화시킨 theta로 구성된 방정식을 나타내는 선이다. 해당 선은 아직 training 과정을 거치지 않은 것이기에 빨간색점과 파란색점을 잘 구분시켜주지않는다. 그러므로 우리는 위에서 최적의 theta를 찾기 위하여 training 과정을 거쳤으며 최적의 theta 값을 찾았다. 최적의 theta로 구성된 방정식은 굵은 점선으로 되어있다. 확연하게 얇은 점선으로 되어있는 방정식보다 training 과정을 거친 굵은 점선으로 되어있는 방정식이 빨간색점과 파란색점을 잘 구분시켜주는 것을 확인할 수 있다. 이로써 우리는 위에서 구한 theta가 학습(training)이 잘이루어졌으며 최적의 theta임을 확인할 수 있다.

Logistic Regression
Logistic Regression을 구현하기위하여 가설함수와 비용함수에 대해서 먼저 알아본다. 가설함수 전체 식은 아래와 같으며, sigmoid 함수가 사용된다.


Logistic Regression의 비용함수 전체 식은 아래와 같다.

비용함수를 미분하게 되면 식은 아래와 같다.

처음에 theta를 [-0.03, -0.01, 0.01] 이라고 초기화시켜준다. 초기화 시킨 상황에서 비용함수의 값은 아래와 같이 출력되는 것을 확인할 수 있다.
초기의 theta를 이용하여 미분한 비용함수값은 아래와 같이 출력되는 것을 확인할 수 있다.
Result : Check results as iteration increases
아래와 같이 설정한 환경속에서 theta를 최적화시켰으며, 업데이트에 소요된 시간은 약 0.03초 정도임을 알 수 있다.
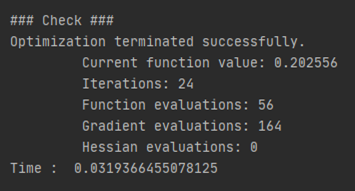
해당 iteration동안 업데이트된 최적의 theta값은 아래와 같이 출력되는 것을 확인할 수 있다.

그래프로 시각화하해보면 아래와 같은 그래프를 확인할 수 있다. 해당 그래프를 보면 얇은 점선으로 되어있는 것은 무작위로 설정함으로써 초기화시킨 theta로 구성된 방정식을 나타내는 선이다. 해당 선은 아직 training 과정을 거치지 않은 것이기에 빨간색점과 파란색점을 잘 구분시켜주지않는다. 그러므로 우리는 위에서 최적의 theta를 찾기 위하여 training 과정을 거쳤으며 최적의 theta 값을 찾았다. 최적의 theta로 구성된 방정식은 굵은 점선으로 되어있다. 확연하게 얇은 점선으로 되어있는 방정식보다 training 과정을 거친 굵은 점선으로 되어있는 방정식이 빨간색점과 파란색점을 잘 구분시켜주는 것을 확인할 수 있다. 이로써 우리는 위에서 구한 theta가 학습(training)이 잘이루어졌으며 최적의 theta임을 확인할 수 있다.

또한 logistic regression의 decision boundary를 시각화하면 아래와 같이 확인할 수 있다.

Comparison : Are two models (Perceptron and Logistic regression) close?
Perceptron에서 구한 theta로 구성된 방정식인 얆은 점선과 Logistic regression에서 구한 theta로 구성된 방정식인 굵은 점선을 비교해보면 아주 유사한 것을 아래 그림에서 확인할 수 있다. 즉, 두개의 theta가 잘 정규화된 것을 확인할 수 있다.

Predict and Accuracies
학습된 parameter를 이용하여 training dataset에 없는 test dataset으로 결과를 예측해보려 한다. test dataset은 data_test.txt 파일을 불러와 training dataset처럼 test1, test2, accepted로 구분하여 testData라고 정의하고 3행으로 shape를 변경해준다. Training accuracy와 Test accuracy를 구하면 아래와 같이 출력되는 것을 확인할 수 있다.

K-Nearest Neighbors (K-NN)
K-NN에서 클래스를 분류할 때의 전체 식은 아래와 같다.

K-NN에서 클래스를 분류할 때 euclidean distance 값을 사용하며, 식은 아래와 같다.

지금까지는 bias term을 위하여 data에 행을 추가하였지만, K-NN에서는 그럴 필요가 없으므로 행을 추가하지않은 데이터를 이용한다. 그러므로 trainX와 testX의 shape은 (80, 2)이다.
KNN_model.py 하위에 있는 euclideanDistance 함수
euclideanDistance 함수를 코드로 구현하면 아래와 같다.

KNN_model.py 하위에 있는 getKNN 함수
getKNN 함수에는 euclidean distance를 이용하여 거리를 구한 후, 가장 가까운 거리에 있는 k개 만큼을 closest_data안에 저장하여 retrun해주는 코드가 구현되어있으며 아래와 같다.

KNN_model.py 하위에 있는 predictKNN 함수
predictKNN 함수에는 getKNN 함수를 통해 구한 k개 만큼이 저장된 data에 Accepted을 의미하는 1과 Not accepted를 의미하는 0 중 빈도수가 높은 값을 따르도록 함으로써 예측해야하는 값의 클래스를 분류한다.

Result : predict class using KNN algorithm
KNN 알고리즘을 이용하여 클래스가 분류된 결과를 시각화하면 아래와 같다.

여기서는 3개의 가까운 값들을 고려하여 예측하였기에 k는 3이며 training accuracy는 0.95 인것을 확인할 수 있다.

Result : Change k value in KNN algorithm
위에서는 k 값을 3으로 설정한 결과만을 확인하였다. 이번에는 k를 1, 5, 20, 40으로 설정하여 결과를 확인해보려 한다. 왜냐하면 우리는 KNN algorithm을 이용하여 클래스를 잘 분류하기 위해서는 적절한 k개를 구해야하기 때문이다. K가 작은 값일 수록, bias는 감소하고, variance는 증가함으로써 Overffiting을 유발한다. 반면 K가 큰 값일 수록, bias는 증가하고, variance는 감소함으로써 Underfitting을 유발한다. 그러므로 적절한 K값을 정하는 것은 중요하다. (참고링크) https://s5unnyjjj.tistory.com/63?category=939071
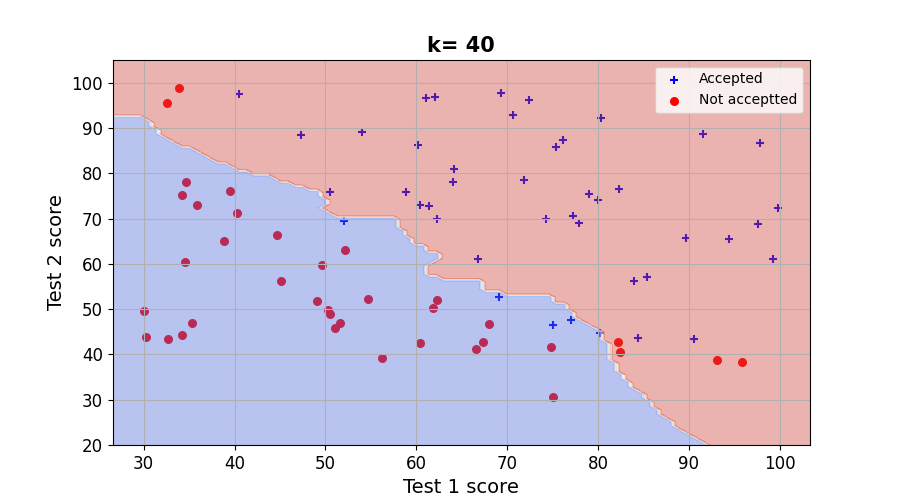
그 결과, k가 1, 5, 20, 40 때의 결과를 시각화하면 아래와 같다. k가 커질수록 decision boundary가 스무스 해지는 것을 확인할 수 있다.



Result : Check training accuracy and test accuracty according to the value of k
k 값에 따른 training accuracy를 그래프로 나타내면 아래와 같다. k가 1이라면 가장 가까운 1개의 값만을 고려하여 예측하는 것이기 때문에 trainin error는 0이 되는 것을 확인 할 수 있다.

k 값에 따른 test accuracy를 그래프로 나타내면 아래와 같다. 해당 그림을 통해 우리는 k가 무조건 작다고 좋은 것도 아니고 무조건 크다고 좋은 것도 아니며 적절한 k 값을 찾는 것이 중요하다는 것을 한번 더 확인 할 수 있다.

----------------------------------------------------------------------------------------------------
>> 위 내용은 필자가 직접 작성한 내용입니다.
>> 필자가 직접 구현한 코드를 아래의 링크에 업로드하였으니 참고바랍니다.
https://github.com/s5unnyjjj/ML_Practice-2
>> 부족한 점이 많을 수 있기에 잘못된 내용이나 궁금한 사항이 있으면 댓글 달아주시기 바랍니다.
>> 긴 글 읽어주셔서 감사합니다.




