ML - Practice #1 : Linear regression, Ordinary Least Squares(OLS), Batch Gradient descent, Stochastic Gradient descent

본 글에서는 아래에 나열된 이론을 바탕으로 코드를 작성해보도록 한다.

 1. Linear regresison (참고링크) https://s5unnyjjj.tistory.com/39?category=939071 

 2. Ordinary Least Squares (OLS) (참고링크) https://s5unnyjjj.tistory.com/33?category=939071 

 3. Batch Gradient descent

 4. Stochastic Gradient descent

 

Used train data

사용할 데이터는 data_train.txt파일에 담겨 있다. 해당 파일을 열어보면 아래와 같이 저장되어있다. 

 

아래의 코드를 이용하여 data_train.txt 파일에서 데이터를 불러온 후, 1행은 population으로 2행은 profit으로 이름을 부여한다.

그렇게 되면 trainData의 5개의 값만 보게되면 아래와 같이 보여진다.

 

trainData의 값들은 아래와 같이 분포 되어 있다.

trainData의 population값들은 trainX라 정의하고, profit값들은 trainY라 정의한다. trainX 값과 trainY 값은 77개이며, shape은 (77, 1)이다. trainX의 shape을 한 차원 증가시키고 첫 행은 1로 초기화 시키면 trainX의 shape은 (77, 2)이다. trainX의 5개의 값만 보게되면 아래와 같이 보여진다.

이로써 우리는 data_train.txt 파일 내에 있는 값들을 전처리 시킨 값을 trainX, trainY라 정의하였으며, trainX의 shape은 (77, 2)로 변경하였다. 이제부터는 trainX와 trainY를 이용하여 코드를 직접 구현해보도록 한다.

 

Linear regression

scikit-learn 이란? scikit-learn (사이킷런)은 파이썬 머신러닝 라이브러리 중 가장 많이 사용되는 라이브러리로 파이썬 기반의 머신러닝 관련 코드 작성 시 유용한 라이브러리이다. 예를 들어 Linear regression는 scikit-learn에서 제공하기에 다수의 코드를 작성하지 않고 한줄의 코드로도 Linear regression을 쉽게 구현할 수 있다. 하지만 여기서는 지금까지 배운 이론을 바탕으로 코드를 구현하고 이론이 맞다는 것을 실습을 통해 완벽히 이해할 것이기 때문에 scikit-learn 없이 구현해보도록 한다. 다만, 우리는 여기서 scikit-learn 없이 구현 해본 후에 구현 결과와 scikit-learn으로 구현 한 결과가 같은지 확인해보도록 할 것이다.

 

Without scikit-learn

Linear regression을 구현하기위하여 가설함수와 비용함수에 대해서 먼저 알아본다. (개념은 아래 더보기에 있음)

가설함수(hypothesis) vs 비용함수(cost function)

 

가설함수(hypothesis)는 training dataset에 없는 새로운 데이터를 입력으로 넣었을 때 예측되는 출력을 도출하도록 하는 함수이다. 

비용함수(cost function)는 predict value와 target value의 오차가 작은 가설함수를 도출하기 위해 사용되는 함수이다.

Linear regression의 가설함수 전체 식은 아래와 같다.

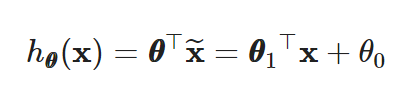
Linear regression의 비용함수 전체 식은 아래와 같다.

 

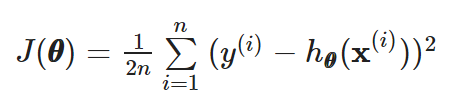
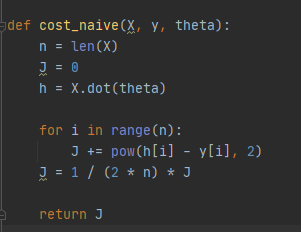
LinearRegression_model.py 하위에 있는 cost_naive 함수

cost_naive 함수에는  loop statement를 이용하여 Linear regression의 비용함수(cost function)을 구현한다. 구현하면 아래와 같다. 

 

 

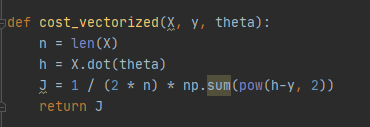
LinearRegression_model.py 하위에 있는 cost_vectorized 함수

cost_vectorized 함수에는  loop statement를 이용하지않고 Linear regression의 비용함수(cost function)을 구현한다. 구현하면 아래와 같다.

 

 

Result: cost_naive (vs) cost_vectorized

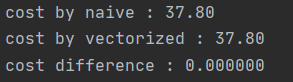
cost_naive 함수를 이용하여 구한 비용함수와 cost_vectorized 함수를 이용하여 구한 비용함수의 값은 같아야하며, 실행 결과 37.80으로 같은 것을 확인할 수 있다.

With scikit-learn

Soon...

 

Ordinary Least Squares (OLS)

Ordinary Least Squares (OLS)의 비용함수 전체 식은 아래와 같다.

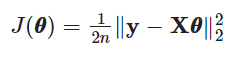
OLS의 theta 구하는 식은 아래와 같다. 해당 theta를 구하는 과정은 다른 글에서 다루었기에 본 글에서는 생략한다. (참고) https://s5unnyjjj.tistory.com/33?category=939071 

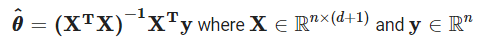
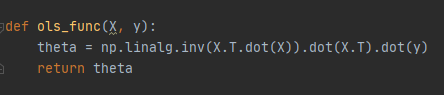
LinearRegression_model.py 하위에 있는 ols_func 함수

ols_func 함수는 OLS의 theta를 구하여 return해주는 함수이므로 위에 작성되어있는 OLS의 theta 구하는 식을 코드로 작성하면 아래와 같다.

 

y= ax + b 라면 해당 theta에는 a와 b가 배열로 저장되어있다. 그러므로 OLS theta 0과 OLS theta 1을 출력해보면 아래와 같이 출력되는 것을 확인할 수 있다.

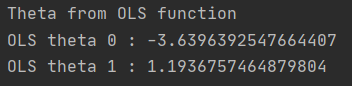
구한 OLS theta 0과 OLS theta 1로 완성된 일차방정식을 training dataset이 분포되어 있는 그래프에 그려보면 아래와 같다.

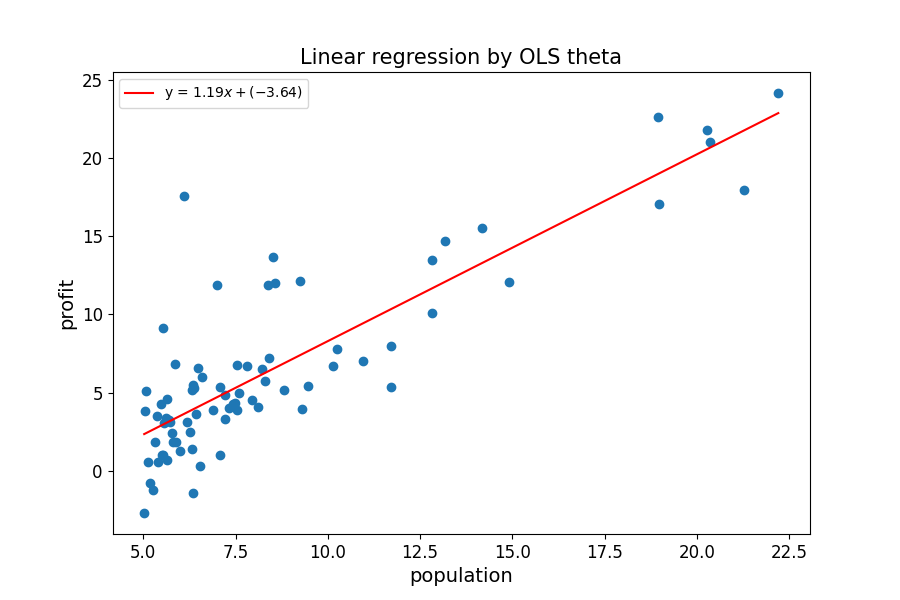
LinearRegression_main.py 하위에 있는 func_visual 함수

func_visual 함수에서는 어떤 theta를 선택하냐에 따라 cost가 얼마나 다양해지는지를 시각적으로 아래와 같이 확인할 수 있다.

 

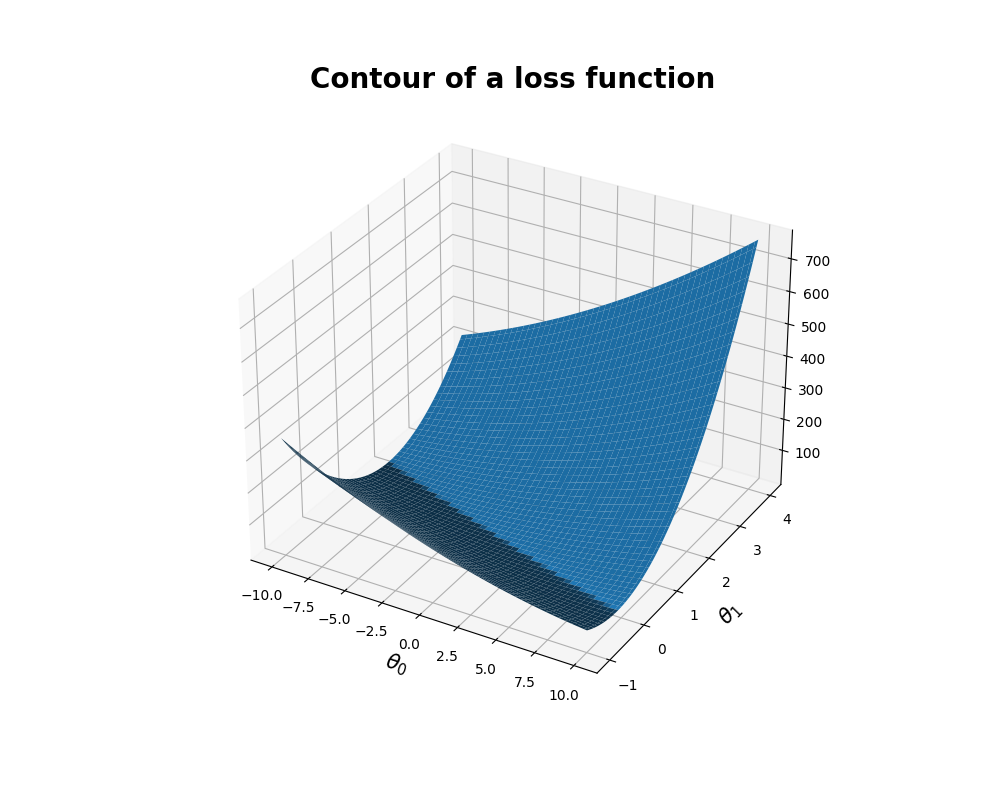
Batch Gradient descent

위에서 알아봤던 비용함수는 predicted value와 target value간의 오차를 평균낸 값이다. 이제부터는 해당 오차를 이용하여 parameter theta를 조절함으로써 오차를 줄이는 작업을 진행할 것이다. 우선 Batch 단위로 theta를 update하는 Batch Gradient descent를 구현할 것이다. Batch Gradient descent에서는 각 iteration에서 theta를 아래 식으로 업데이트 해나간다.

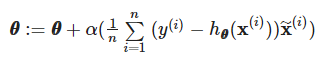
앞서 말했듯이 theta를 update하기 위해서는 비용함수의 값이 필요하다. 우리는 앞서서 cost_naive 함수와 cost_vectorized 함수, 총 2개의 함수를 이용하여 비용함수를 구했으며 값이 같은 것을 확인하였다. theta를 update하기위해서 cost_naive함수를 이용하여 theta를 update하는 방법과 cost_vectorized함수를 이용하여 theta를 update하는 방법 총 2개의 방법을 진행해볼 것이다. (여기서는 theta를 update하기위한 iteration은 3000, alpha는 0.01로 초기화시켜주고 시작한다.)

 

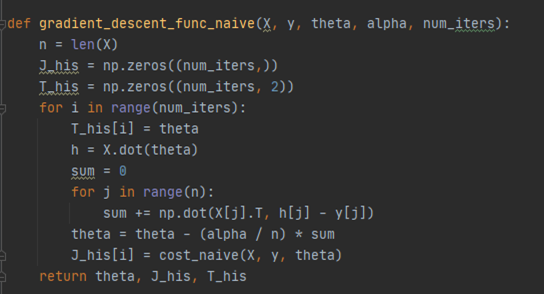
LinearRegression_model.py 하위에 있는 gradient_descent_func_naive 함수

gradient_descnet_func_naive함수에는 cost_naive함수를 이용하여 theta를 update하는 코드를 구현한다. 구현하면 아래와 같다.

 

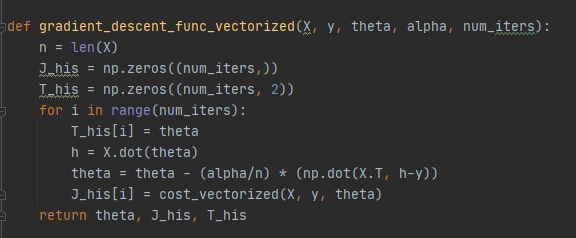
LinearRegression_model.py 하위에 있는 gradient_descent_func_vectorized 함수

gradient_descent_func_vectorized함수에는 cost_vectorized함수를 이용하여 theta를 update하는 코드를 구현한다. 구현하면 아래와 같다.

 

Comparison : which version is faster, func_naive or func_vectorized?

gradient_descent_func_naive함수를 이용하여 updated theta와 gradient_descent_func_vectorized함수를 이용하여 updated theta 값이 같은 것을 확인할 수 있다. 하지만 후자 함수를 이용한 것이 속도가 더 빠른 것을 확인할 수 있다. 

 

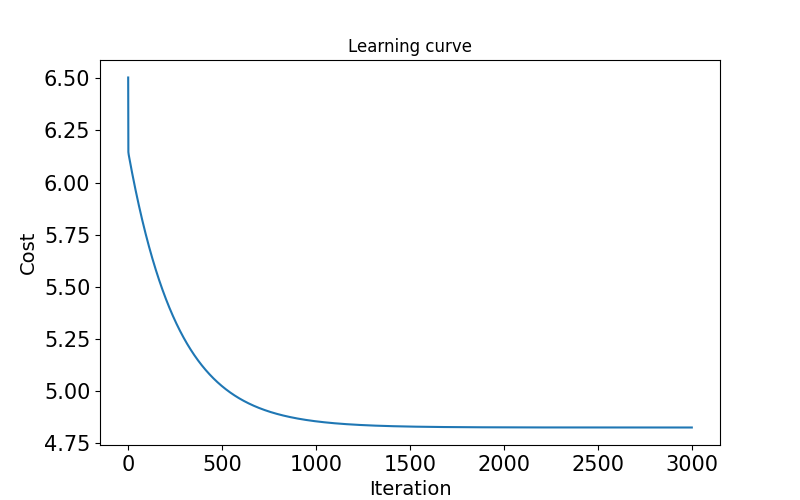
Result : Check results as iteration increases

iteration이 증가할 때마다 오차를 의미하는 cost 값이 줄어드는 것을 확인함으로써 학습이 올바르게 이루어진 것을 확인할 수 있다.

 

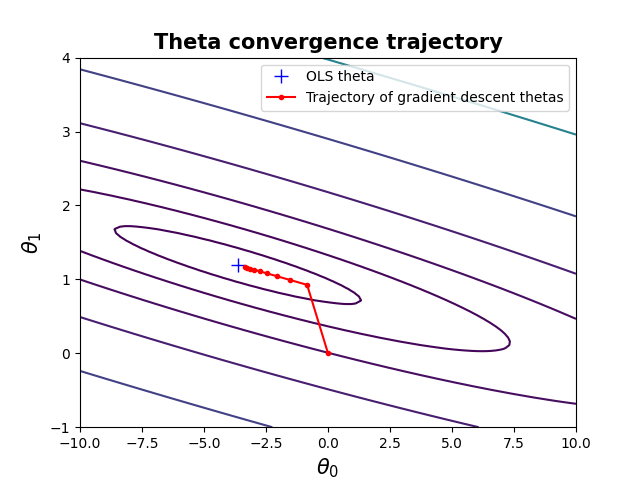
theta를 update함으로써 OLS theta인 파란색에 빨간색 값이 점점 수렴하는 것을 확인할 수 있다.

 

파란색 선은 target으로 하는 방정식이며, 빨간색으로 우리가 학습해야할 방정식이다. 500 iteration마다 확인해보면 빨간색 선이 점점 target으로 하는 파란색 선에 가까워지다가 마침내 포개지는 것을 확인할 수 있다.

 

Stochastic Gradient descent (SGD)

이번에는 Batch 단위가 아닌 Stochastic 단위로 theta를 update하는 Stochastic Gradient descent를 구현할 것이다. Stochastic Gradient descent는 batch가 1이기에 n으로 나눠주지 않으며 theta를 아래 식으로 업데이트 해나간다.

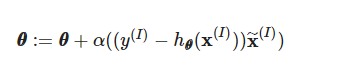
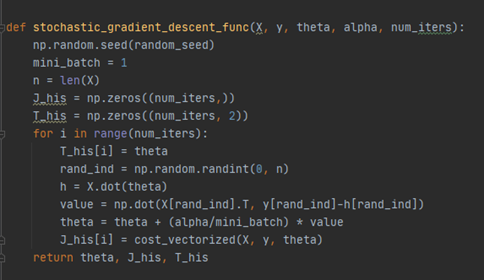
LinearRegression_model.py 하위에 있는 stochastic_gradient_descent_func 함수

stochastic_gradient_descent_func함수에는 1 batch단위로 theta를 update하는 코드를 구현한다. 구현하면 아래와 같다.

 

 

Result : Theta by Stochastic Gradient descent (SGD)

Stochastic Gradient Descent를 이용하여 구한 theta 값은 아래와 같이 확인할 수 있다.

 

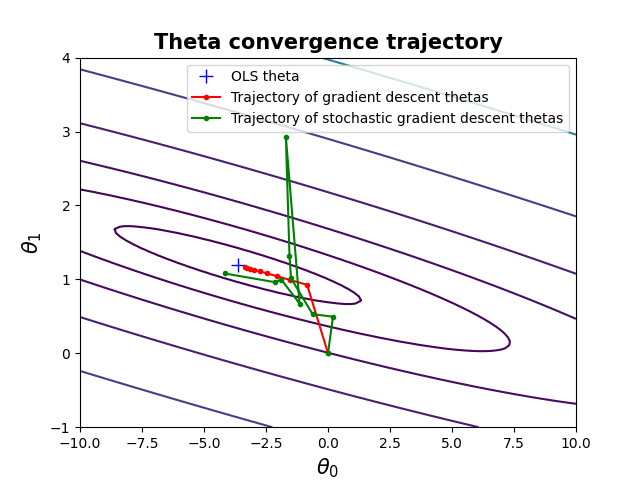
Result : Theta by Stochastic Gradient descent (SGD)

Stochastic Gradient Descent는 Batch Gradient descent인 빨간색 선에 비해 안정적으로 수렴하지 않고 이리저리 요동치며 수렴하는 것을 확인할 수 있다. 하지만 Stochastic Gradient Descent는 Batch Gradient descent에 비해 계산적으로 효율적이라는 장점을 갖고 있다.

 

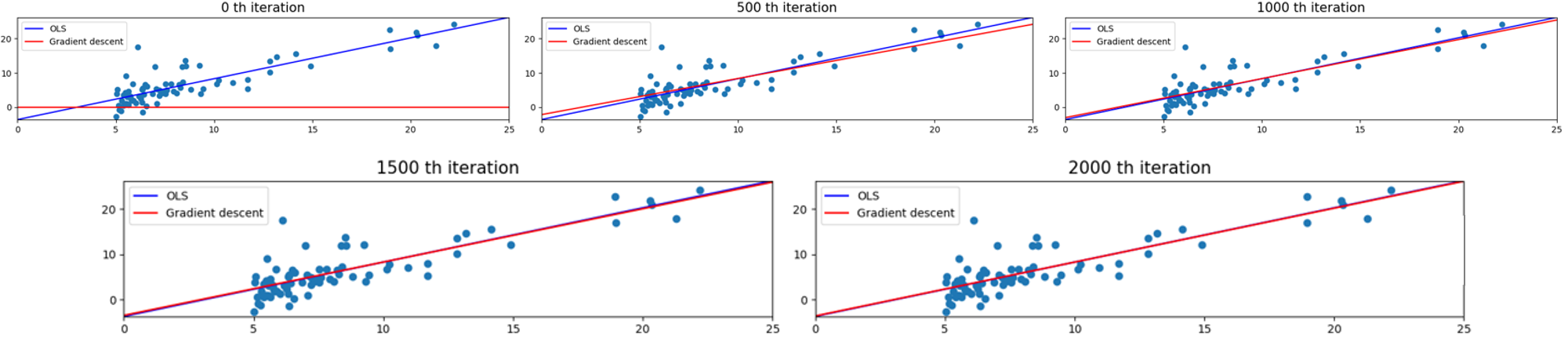
파란색 선은 target으로 하는 방정식이며, 빨간색으로 우리가 학습해야할 방정식이다. 500 iteration마다 확인해보면 빨간색 선이 점점 target으로 하는 파란색 선에 가까워지다가 마침내 포개지는 것을 확인할 수 있다.

 

Predict and Accuracies

학습된 parameter를 이용하여 training dataset에 없는 test dataset으로 결과를 예측해보려 한다. 또한 training MSE와 test MSE도 계산해볼 것이다.

아래 그림에서 파란색 점은 training dataset이며 빨간색 점은 population 7.5와 15라는 값이며 예측해야하는 값이다.

 

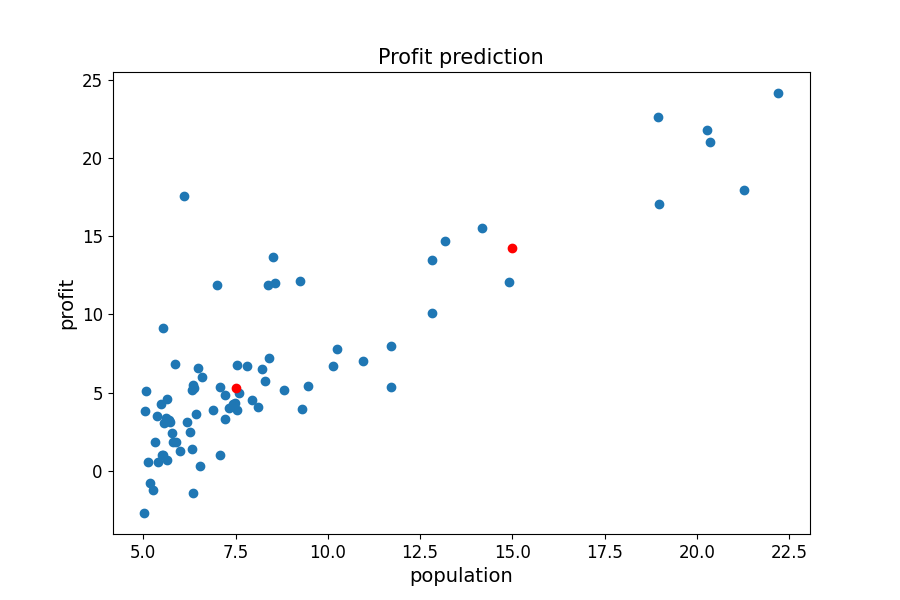
test dataset은 data_test.txt 파일을 불러와 training dataset처럼 population과 profit으로 구분하여 testData라고 정의하고 2행으로 shape를 변경해준다.

OLS의 theta를 이용하여 예측한 predicted value와 training target value 간의 MSE와 Batch gradient descent의 theta를 이용하여 예측한 predicted value와 training target value 간의 MSE는 아래와 같이 확인할 수 있다.

 

OLS의 theta를 이용하여 예측한 predicted value와 training test value 간의 MSE와 Batch gradient descent의 theta를 이용하여 예측한 predicted value와 training test value 간의 MSE를 아래와 같이 확인함으로써 어느 모델이 일반화가 잘되었는지 확인할 수 있다.

 

 

----------------------------------------------------------------------------------------------------

 

>> 위 내용은 필자가 직접 작성한 내용입니다.

>> 필자가 직접 구현한 코드를 아래의 링크에 업로드하였으니 참고바랍니다.

https://github.com/s5unnyjjj/ML_Practice-1

>> 부족한 점이 많을 수 있기에 잘못된 내용이나 궁금한 사항이 있으면 댓글 달아주시기 바랍니다.

>> 긴 글 읽어주셔서 감사합니다.